目次
はじめに
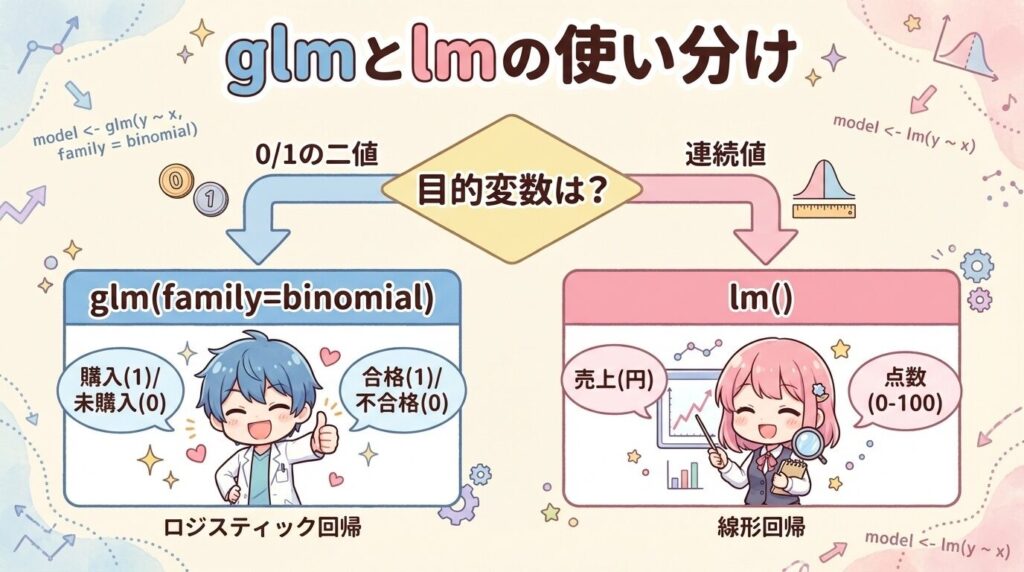
「このデータってglmでロジスティック回帰をしていいの?」「Rでどう選べばいいのか迷う…」と感じたら、まずは目的変数が0か1の二値になっているかを見てみてください。結果が「はい/いいえ」「成功/失敗」のように2つに分かれるなら、family=binomialを指定してglmを実行しますし、売上や点数のように数値そのものを予測したい場合は、ロジスティック回帰ではなく別の回帰方法に切り替えます。
実行したあとはsummaryに表示される数値を一つずつ確認し、「この変数は残してよさそう?」「外したほうが分かりやすいかな?」と手元の結果を見ながら整理していきましょう。つまずきやすいのは、モデルをどれにするか考えるところ、binomialの指定を入れるところ、そして結果の数値を読み取るところです。ここでは、そうした迷いを一つずつ解消していけるように、順番に見ていきますね。
glmでロジスティック回帰にするのはどんなとき?lmとの使い分けは?
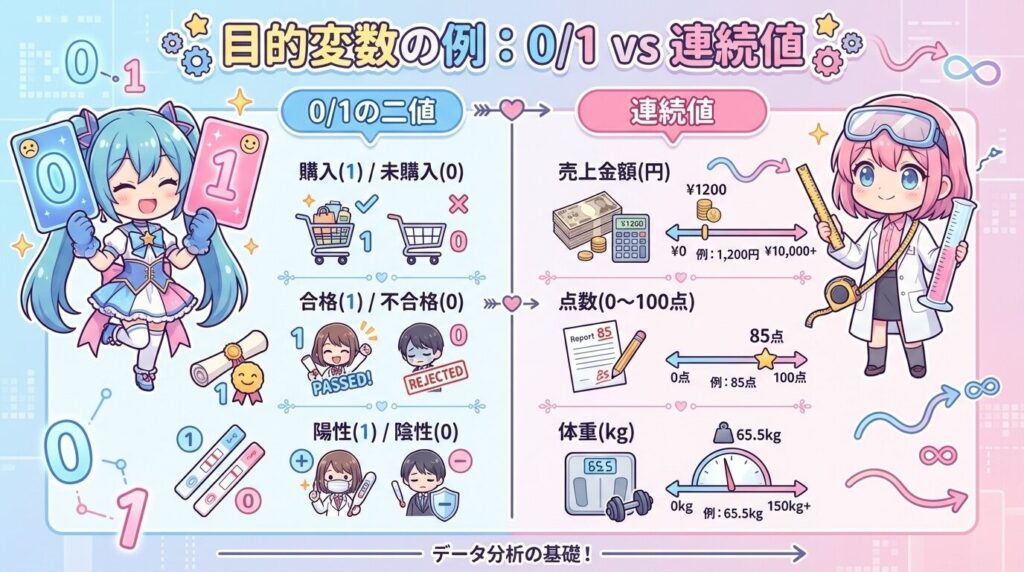
目的変数が「0/1(はい・いいえ)」のように2値なら、lmではなくglm(ロジスティック回帰)を選びます。たとえば「購入した/していない」「合格/不合格」「病気あり/なし」のように、結果がどちらかに決まるデータです。
一方で、売上金額や身長のように数値が連続していて、そのままの値を予測したいならlmを使います。まずは目的変数が2値か連続値かを確認し、2値ならglm、連続値ならlmに切り替えてください。
目的変数が0/1の二値ならglmでロジスティック回帰を選ぶ
(購入した/していない)のように結果が0か1のどちらかで固定されているなら、まず目的変数の列を開いて「0と1しか入っていない」ことを確認します。OKなら、結果を“数値として当てにいく”のはやめて、1(購入した)になる確率を出す形でモデルを組みます。
たとえばアンケートで「購入した=1/購入していない=0」が300件あり、説明変数に「年齢」「広告クリック回数」「サイト滞在時間」などがある場合は、glmでfamily=binomial(logit)を指定してロジスティック回帰を回します。出てくる予測値が0.82なら「購入する確率82%」のように読めるので、確率が高い人を優先して案内する・低い人には別の施策に切り替える、といった使い方にそのまま繋げられます。
売上金額や点数などの連続値ならlmで通常の回帰を選ぶ
売上金額やテストの点数のように、0/1ではなく数値そのものが上下する列を目的変数に使う場合は、まずデータを開いて「金額や点数が連続して並んでいるか」を確認します。売上が1,000円〜5,000円まで細かく動いている、テストの点数が32点・74点・88点のように幅を持っているなら、結果を確率ではなく数値としてそのまま予測します。
たとえば「広告費」「来店回数」「滞在時間」から売上金額を予測したい場合は、lmで通常の回帰モデルを作成します。予測結果が3,200円のように具体的な金額として出るため、ロジスティック回帰のように0か1へ丸める必要はありません。点数や金額を直接出したいときは、glmの二値モデルは使わず、lmで数値の変化をそのまま扱います。
R言語でロジスティック回帰glmを書くときに必ず入れる設定
Rでロジスティック回帰をglmで書くときは、まずfamily=binomialを指定して、目的変数が0と1で表されているかを確認してください。購入の有無や成功・失敗のように結果が2つに分かれるデータであれば、この形にそろえてから式を書き始めます。目的変数が数値のまま連続値になっている場合は、そのまま実行せず、0/1の形式に整えてからglmを入力します。
family=binomialを指定してglmを実行する
目的変数が0/1の二値で、「1(成功・購入など)になる確率」を出したいときは、glmでfamily=binomialを指定して実行します。まず自分のデータ名と列名をそのまま当てはめて、次の形で打ちます。
model <- glm(y ~ x, data = データ名, family = binomial)たとえば「購入した=1/購入していない=0」をbuy列に入れていて、説明変数がageとclickなら、glm(buy ~ age + click, data = df, family = binomial)のように書きます。実行したら、コンソールに赤字のエラーが出ていないかを確認し、何も出ずに処理が終わればモデル作成は完了です。モデルが作れたら、summary(model)で係数や有意性を確認する準備が整います。
目的変数を0/1の二値に整形してからglmを実行する
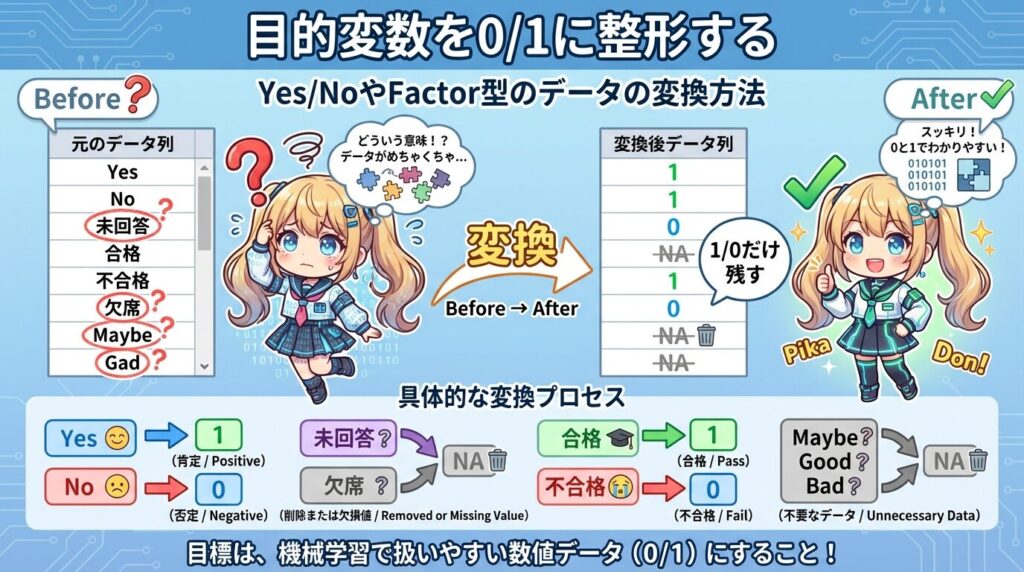
glmでロジスティック回帰を回す前に、目的変数の列を開いて0/1になっているかを先に揃えます。読み込んだ直後は「Yes/No」「合格/不合格」「購入/未購入」のように文字やカテゴリのまま入っていることが多いので、そのままfamily=binomialを指定すると途中で止まります。
たとえば目的変数がresult列で「Yes」「No」が入っているなら、Yes=1・No=0のように対応を決めて、実行前に列を0/1へ変換します。変換後に目的変数の中身が0と1しかないことを確認できたら、はじめてglm(result ~ ..., data=..., family=binomial)を実行します。ここを先に整えておくと、glmの実行で余計なエラーに引っかからず、結果の解釈(確率として読む)まで一気に作業を進められます。
Yes/NoやFactor型のままなら0/1に変換できるまで進まない
目的変数の列を開いて、「Yes」「No」やFactor型のままになっていないかを先に確認します。もしYes / No / 未回答のように3種類以上の値が混ざっていたり、1・2・3のような数字が並んでいる場合は、そのままpredictを実行しません。まず「Yes=1」「No=0」のように対応を決めて、目的変数の列を0か1だけが入る数値列に作り替えます。
たとえばresult列に「Yes」「No」が入っているなら、変換後にtable(result)で0と1しか表示されない状態まで整えます。列の中身が0と1だけになったのを確認してから、glmやpredictを実行します。ここを先に揃えておくと、予測確率が0.73のように数値で返ってくるため、成功しそうなデータだけを抽出する操作までスムーズに続けられます。
R言語ロジスティック回帰glmのsummary結果をこの順番で確認する

glmを実行したら、まずsummary()を開き、画面に出た数値を上から全部読むのではなく「見る場所」を先に決めて確認してください。係数表(Coefficients)では、行ごとのEstimateとPr(>|z|)など、必要な列だけに目を向けます。次に、モデル全体の当てはまりとしてNull devianceとResidual devianceの差を見て、最後にAICを確認します。ここまで見て「このまま使うか、説明変数や式を見直すか」を判断し、必要ならモデル式を書き直してからもう一度summary()を開きます。
① Estimateの符号で影響の向きを確認する
summary(model)を開いたら、まず**Estimateの列の「+か−か」**だけを順番に見ていきます。Estimateがプラスなら、その説明変数が増えるほど「成功(1)」の確率が上がり、マイナスなら確率が下がる方向へ動いています。
たとえばclickのEstimateが+0.85ならクリック数が多いほど購入に近づき、ageが-0.40なら年齢が上がるほど購入から離れる方向に影響していると読み取れます。まずは符号だけを一覧で確認して、想定と逆の向きになっている変数があれば、その列の中身や符号の付け方(0/1の定義や前処理)を見直します。数値の大きさやp値を見る前に、向きが合っているかをここで整えておくと、その後の解釈がブレずに進みます。
② p値を見て残す変数と外す変数を決める
summary(model)を開いたら、次にPr(>|z|) の列を上から順に確認します。ここでは「予測に使う説明変数を絞る」作業だけをやります。0.05より小さい行の変数だけを残し、0.05以上の変数は一度モデルから外します。
たとえばclickのp値が0.003なら残し、ageが0.42、genderが0.18ならいったん外します。全部を残したままpredictを走らせず、残した変数だけの式に書き直して、もう一度glmを実行します。変数を減らした状態でモデルを作り直しておくと、予測確率を出したあとに「結局どの変数が効いているのか」で迷わずに済みます。
③ exp()でオッズ比に変換して影響の大きさを確認する
Estimateの数値が直感的に読みづらいときは、exp(coef(モデル名))を実行してオッズ比に変換します。たとえばmodelという名前でglmを作っているなら、exp(coef(model))と入力すると、各説明変数がどれくらい影響しているかを倍率で確認できます。
表示された数値は1を基準に見ます。click = 1.80ならクリック数が増えるほど成功確率が上がる方向に働き、age = 0.65なら年齢が増えるほど成功確率が下がる方向に影響しています。まずは1より大きいか小さいかだけを並べて確認し、どの変数が強く効いているかを把握します。ここでは倍率の比較だけを行い、追加の検定や別の操作には触れずに、影響の大きい変数の整理まで進めます。
R言語ロジスティック回帰glmで予測確率をpredictで出力する
glmでモデルを作成したら、predict()を使って「どのくらいの確率で1になるか」を数値として取り出します。分類ラベルではなく確率を見たい場合は、type="response"を指定して出力してください。新しいデータで確率を出したいときはnewdataにデータフレームを渡し、学習に使ったデータに確率を追加したい場合は、元のデータにそのまま結果を代入します。ここまでできれば、予測確率の確認としては十分です。
predict(type="response")で各データの予測確率を出力する
モデルを作成したら、各データが「成功(1)」になる確率をそのまま確認します。modelという名前でglmを保存しているなら、次のように入力します。
prob <- predict(model, type = "response")表示される数値は0から1の間になり、0.72なら「成功する確率72%」、0.18なら「成功する確率18%」としてそのまま読めます。ここでtype="response"を指定せずに実行すると、対数オッズ(link値)が出てしまい、そのまま確率として使えません。必ずtype="response"を付けて、0〜1の値になっていることを確認してから次の処理に進みます。
出力した確率を0.5または任意の閾値で分類する
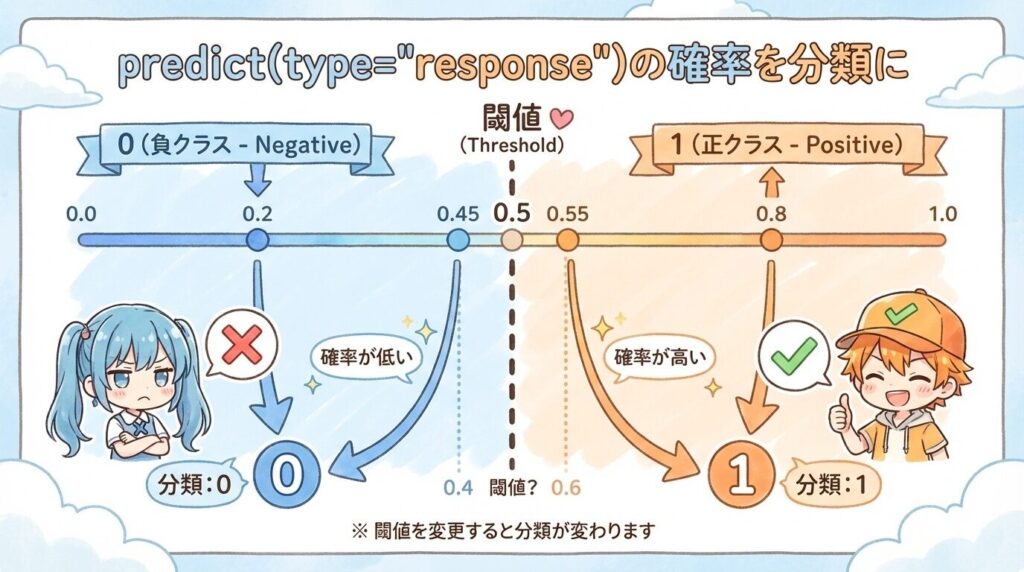
predict(type="response")で出した確率を、0/1の判定に置き換えて使います。まずは0.5以上を1、0.5未満を0として分類し、結果は元データに新しい列として追加します。たとえば確率が0.72の行は1(成功)にし、0.31の行は0(失敗)にします。
0.5で判定して誤判定が目立つ場合は、境界を0.6に上げて「確信が高い行だけを1にする」か、0.4に下げて「取りこぼしを減らす」形に切り替えます。データ数が少ない場合は境界を頻繁に動かさず、0.5の固定値のまま分類して結果を確認します。分類した0/1の列を作っておくと、あとで実測値との比較や集計をそのまま同じ表で行えます。
R言語ロジスティック回帰glmの合格ライン
glmでロジスティック回帰を実行してsummary()の数値を確認し、predict()で確率まで出せたら、まずはそこで作業を止めて大丈夫です。係数表の有意性やAICなどを見て大きな問題がなければ、無理に別の検定や複雑な比較を追加する必要はありません。画面に表示された指標を一通り確認できていて、予測確率が数値として取り出せているなら、そのモデルはひとまず完成として扱えます。追加で評価を行いたいときだけ、ROCや別モデルとの比較に進みます。
summaryの確認と予測確率の出力までできていれば十分
glmを回したら、まずsummary(model)を開いてEstimateの符号とPr(>|z|)のp値を確認します。符号で「成功(1)に近づく/遠ざかる」を押さえ、p値が0.05未満の変数だけを残して読み取れる状態にします。Estimateが読みづらいときはexp(coef(model))を実行し、オッズ比が1より大きいか小さいかだけを見て、影響の強さを把握した時点で止めて構いません。
次にpredict(model, type="response")で各行の予測確率を出力し、0〜1の値をそのまま確率として扱います。たとえば0.73なら「成功確率73%」、0.18なら「成功確率18%」としてそのまま使えます。必要があれば、0.5以上を1、未満を0として分類し、結果を新しい列に追加します。ここまでできていれば、影響の向き・有意な変数・各データの成功確率が一通り揃うので、実務としてはそこで一度区切れます。
AICや理論解説は必要になったときだけ追加する
AICは、モデルを複数作って「どれを採用するか」決めたいときだけ確認します。たとえば説明変数を変えたmodel1とmodel2を用意したら、AIC(model1, model2)のように並べて表示し、数値が小さいモデルを選びます。AICを見ないままでも、summaryで影響の向きと有意な変数を確認できていて、predictで予測確率まで出せているなら、その時点で作業は止めて構いません。
また、この段階でリンク関数や分布族、最尤推定の数式まで読み始める必要はありません。今やっているのが「結果の解釈」と「予測確率の出力」なら、実行結果に直接関係しない理論は追いかけず、必要になったタイミングでだけ追加します。
まとめ
目的変数が「0か1」で分かれているデータなら、glmでロジスティック回帰を使い、family=binomialを指定してモデルを作成します。実行前には目的変数を必ず0/1に整形し、Yes/NoやFactor型のまま残さないようにします。モデルが作れたらsummary()を開き、Estimateの符号で成功側に近づくか離れるかを確認し、Pr(>|z|)のp値を見て0.05未満の変数だけを残します。Estimateが読みづらいときはexp()でオッズ比に変換し、1より大きいか小さいかだけを見て影響の大きさを把握します。
次にpredict(type="response")で各データの予測確率を出力し、0〜1の値をそのまま成功確率として扱います。必要なら0.5を基準に0/1へ分類し、新しい列として追加します。ここまでできていれば、どの変数が影響しているか、成功確率がどれくらいかを実務で使える形まで整理できています。AICの比較や理論的な数式は、複数モデルを並べて選びたい場合だけ確認すれば十分なので、予測確率の出力まで完了した時点で一度作業を区切って問題ありません。